
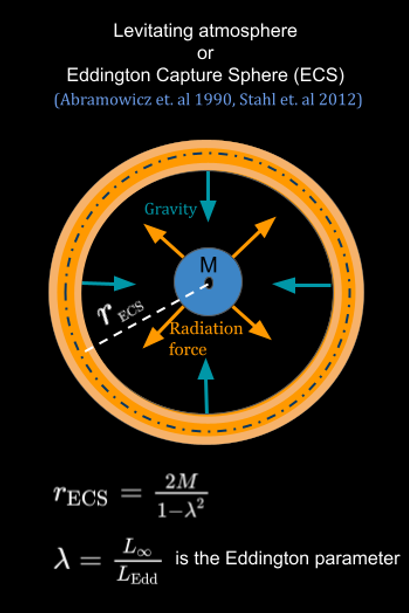
Levitating Atmospheres
Super-Eddington luminous neutron stars are observed in various astrophysical phenomena, powered by the accretion of matter onto the stellar surface or surface nuclear burning. At such high luminosities, stars can potentially harbour “levitating” atmospheres, i.e., atmospheres supported at a certain height above the stellar surface by the radiation pressure from the luminous neutron star. In contrast to Newtonian gravity, where both the radiation force and gravitational force decrease as the inverse square of the radius, in general relativity, the radial dependence of the radiation and gravitational forces differs because of the redshift factors. The radius where these forces balance is called the radius of the "Eddington capture sphere"
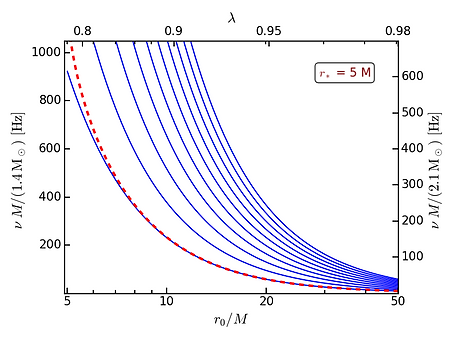
Frequencies (in Hz) of the initial ten normal modes of undamped oscillations of the geometrically and optically thin, levitating atmospheres as a function of the atmosphere location.
Under the assumption of an optically thin limit, the oscillations of such levitating atmospheres can be computed analytically. In Bollimpalli & Kluzniak 2017, we showed that the eigenfrequencies of radial oscillations of geometrically thin, and optically thin levitating atmospheres in Newtonian formalism decrease with increasing luminosity (as shown in the above figure), similar to the observations of X-ray burst oscillations. Interestingly, the ratio of any two eigenfrequencies depends only on the atmosphere’s polytropic index.
Including the radiation drag effects damps the oscillations as reported in Bollimpalli et. al 2019, where we studied the atmospheric oscillations in full general relativity. We found that the oscillation frequency has a characteristic maximum, based on which we propose a new method for accurate simultaneous measurement of both the mass and radius along with the distance to the source. The key result of this work is that the frequency of these oscillations depends only on the stellar parameters and luminosity which allows the direct measurement of the mass and radius, given the observations of maximum frequency and flux (as shown in the figure to the right). However, in this method, the uncertainties in the distance to the source lead to a 10-20% error in mass and radius measurements.
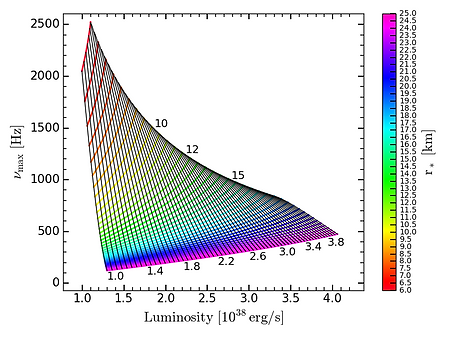
This figure illustrates the mass and radius of the neutron star can be derived from a given luminosity and the frequency of oscillations for the second mode. The ascending lines represent the contours of stellar radius in km, plotted in increasing steps of 0.5 km from top to bottom. The nearly vertical black lines indicate the contours of stellar mass, increasing steps of 0.05 solar mass from left to right.

This figure illustrates how the luminosity, and thereby the distance to the source, are estimated given the mass and radius estimates for the observed frequency maximum. The coloured descending contours represent luminosity (in units of 10^38 erg s−1 ) plotted in steps of 0.1, and the black quasi-diagonal lines represent the frequency maximum contours plotted for every 50 Hz.
An alternative method is to rely on the variation of the two directly observable quantities with respect to each other, i.e., the frequency variation with the flux scaled to the flux at the frequency maximum. With this method, it could be possible to measure the stellar parameters to within < 2% error and also directly determine the distance to the neutron star with an accuracy of about 1% (as shown in the figure to the left).
Such high accuracy measurements of mass and radius of neutron stars have profound implications for constraining the equation of state of dense matter. A more direct implication for Type-I X-ray bursts would be a similar study for optically-thick atmospheres including magnetic fields, which can be achieved through numerical simulations.